这一和二都是以数组模拟为主.因为用数组模拟效率高,

  1. 链表与邻接表(lin邻)
  2. 栈和队列
  3. kmp

①单链表:单链表最大的用途是用来写邻接表.邻接表最大的两个用途是来存储图和树.

②双链表:优化某些题目

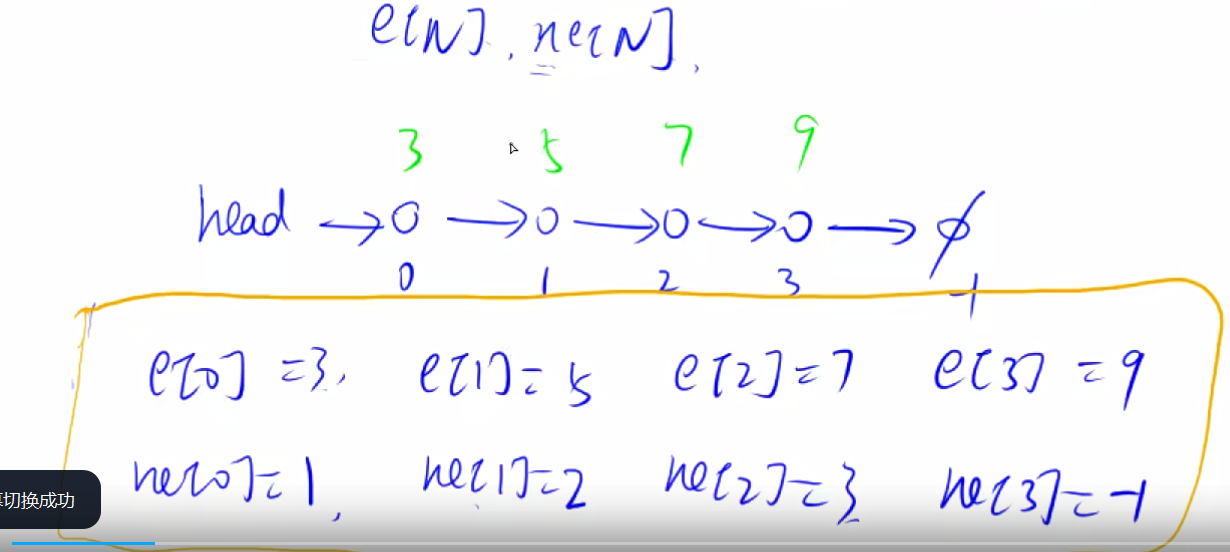
单链表

单链表用数组模拟的情况如图所示

用数组模拟链表,被称为静态链表

image-20241105185824544

不要害怕自己听不懂,听不懂就背嘛,无所谓的.

刚刚自己拿笔和纸花了画图,写了写可能的代码,结果就很清晰,一点疑问都没有.而且还总结出来一个东西,就是

对于指针之间的相互赋值,我一开始总是觉得理解的不够顺畅,现在我明白了.

将指针a赋值给指针b如b = a;其实就是让==b指向 a指向的地方==

通过这段思考,我自己写出了和y总一样的代码,同时可以看到y总一直在说话,所以我也要一直在说话.而且y总也是在不停重复让指针b指向指针a指向的地方就是写成 b = a;(非常地好记忆和理解)

image-20241105130430045

826单链表

有部分讲错了,还好自己看了弹幕,效率很高.

一个弹幕说的很对:head是模拟的头结点/哑结点的指针,这个节点不存放数值,这个节点没有实体,只有指针.

我有一计,不等他讲为啥错,我在CLION里面debug

我错了,我不会用 Clion debug,但是我就在win10下面用vs2017debug也一样.

我懵懵懂懂找出来应该是add()函数的问题,但还是不知道怎么修改.

后来看视频发现是应该写成

1
2
3
4
5
6
7
8
9
10
            add(k - 1, x);
和
    cin >> k;
            if (k == 0)
            {
                head = ne[head];
            }
            else
                remove(k - 1);
        }

个人错误

题干意思里面的第k个数,实际上在我们的数组构成的链表里面对应的下标是k - 1;

所以要把调用函数时候穿进去的实参都写成k - 1;

形参不用改,因为形参是根据我们的模型,也就是数组构成的链表来的,所以形参k就是对下标为k的数进行什么什么操作.

反正你记住一点,形参一般都没问题,都是实参要根据题干意思做特殊处理

尤其是这个条件

D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。

需要if判断一下,if传进去的实参 k = 0,这直接让head = ne[head]

else 让 调用remove(k - 1)//此时k >= 1, 则k - 1 >= 0,对于穿进去的形参而言,>=0是合法的.

正确代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
using namespace std;
const int N = 100010;
// head表示头结点的下标
// e[i]表示节点i的值
// ne[i]表示节点i的next指针是多少,
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
    head = -1;
    idx = 0; // 表示当前可以从零号点开始用,因为没有任何一个点被分配
}
// 将x插到头结点一个算法题里面百分之八十的情况都是插入到头结点后面
void add_to_head(int x)
{
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx++;
}
// 将x插入到下标是k的点后面
void add(int k, int x)
{
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx++;
}
// 将下标是k的点后面的点删掉
void remove(int k)
{
    if (ne[k] == -1) //?y总没写,但是弹幕有人指出这种情况下会出问题,所以我加一个if判断,保证正确性.
        return;
    else
    {
        ne[k] = ne[ne[k]];
    } // 删了一个点,是逻辑上删除,直接当它不存在就行.算法题里面是不需要去管的
}
int main(void)
{
    int m;
    cin >> m;

    init();

    while (m--)
    {
        int k, x;
        char op;
        cin >> op;
        if (op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'I')
        {
            cin >> k >> x;
            add(k - 1, x);
        }
        else
        {
            cin >> k;
            if (k == 0)
            {
                head = ne[head];
            }
            else
                remove(k - 1);
        }
    }

    for (int i = head; i != -1; i = ne[i])
        cout << e[i] << " ";

    return 0;
}

个人感觉没必要自己太主动的学习,直接跟着混视频要答案得了.不然速度太慢了.

而且不要再动不动就切换到ubuntu了,不需要你切换去解决问题.

而且你换来换去容易导致忘记改动win10的时间,然后让上传上去的图片重名(这个问题很严重)

双链表

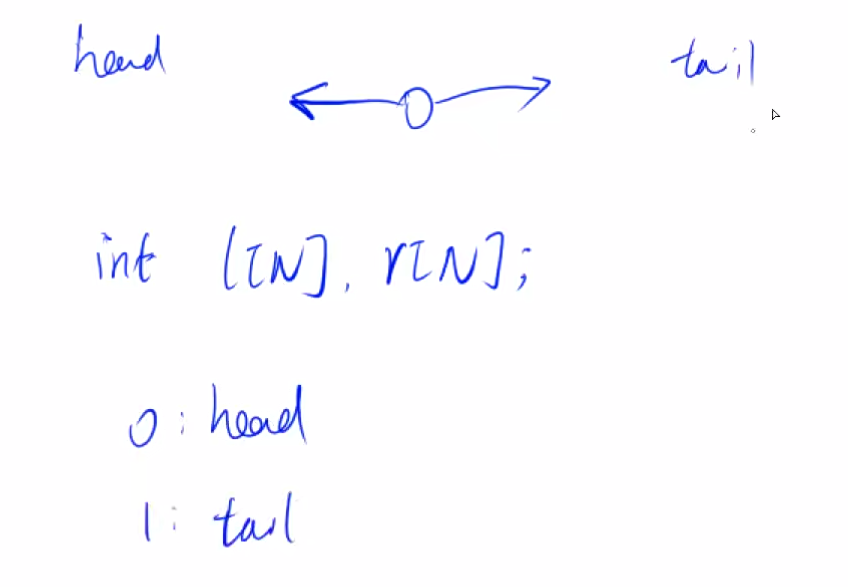
image-20241105130636242

让下标为零的点,是左端点,让下标是1的点,是右端点

下面的无论是插入还是删除,只要你画图,你就会懂了.

插入

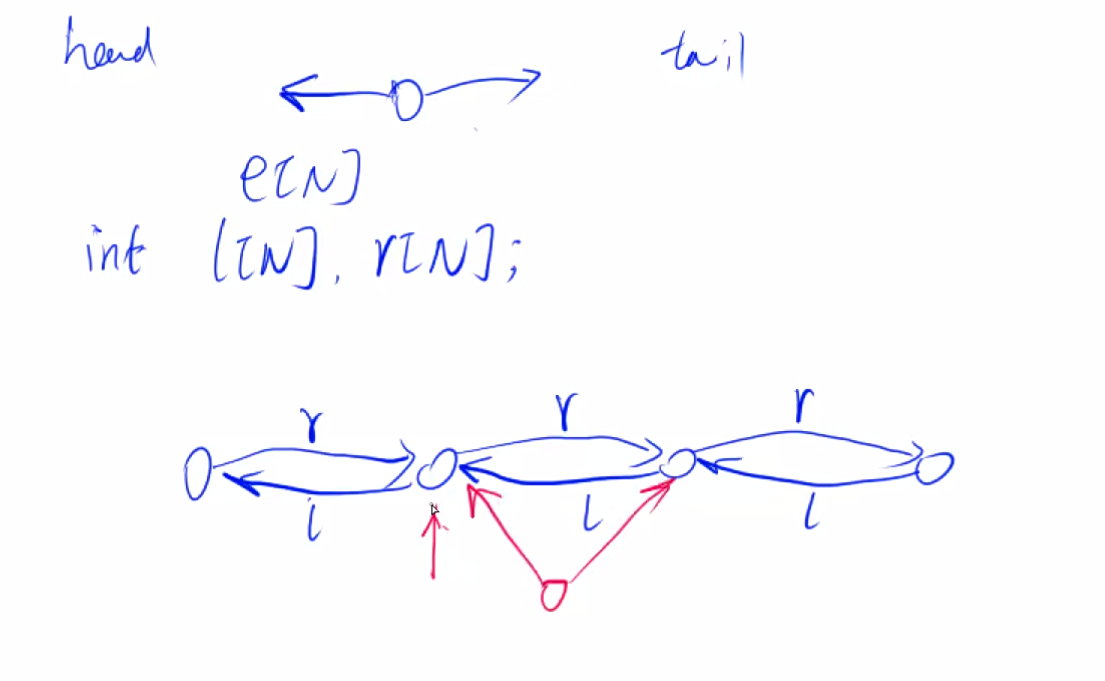
插入的时候先做 让新的要被插入的点指向他能指向的所有点(指针的赋值,同时这些操作都不会影响原来双链表指针的 指向关系)(我说的这个操作就是图里面红色箭头的操作)

然后就是改变原来双链表指针的操作,特别注意顺序,具体自己画图看,

如果你先给k节点的r指针重新赋值的话,会丢失r[k]指向的节点的地址;所以要先给r[k]指向的节点的l指针赋值.

image-20241105211829543

代码就是

1
2
3
4
5
6
7
8
9
10
11
12
13
// 在下标是k的点的右边,插入x
// 如果想在k的左边插入,就把调用函数时的实参k写成l[k]
void add(int k, int x)
{
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];

    // 步骤1和步骤2一定不能写反,原因自己画图看
    l[r[k]] = idx; // 1
    r[k] = idx;    // 2
    idx++;
}

删除

目前的全部

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
using namespace std;
const int N = 100010;

int m;
int e[N], l[N], r[N], idx;
// 初始化
void init()
{
    // 0表示左端点
    // 1表示右端点
    r[0] = 1;
    l[1] = 0;
    idx = 2; // 因为0 和  1已经别占用过 了
}
// 在下标是k的点的右边,插入x
// 如果想在k的左边插入,就把调用函数时的实参k写成l[k]
void add(int k, int x)
{
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];

    // 步骤1和步骤2一定不能写反,原因自己画图看
    l[r[k]] = idx; // 1
    r[k] = idx;    // 2
    idx++;
}
// 删除下标为k的数
void remove(int k)
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}
int main(void)
{

    return 0;
}

正确代码

邻接表

把每个点的所有临边全部存下来.开了n个单链表,邻接表其实就是n个单链表

每一个点head[i]其实存的是第i个点所有的临边,用一个链表给他存起来了.

栈

先进后出

目前的代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>

using namespace std;
const int N = 100010;
int stk[N], tt;
int x;
// 插入一个x
stk[++tt] = x;
// 弹出
tt--;
// 判断栈是不是为空
if (tt > 0)bukong
else kong

// 取出来栈顶元素
stk[tt];
int main(void)
{

    return 0;
}

队列

先进先出

image-20241105215935788

队列的目前全部代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

using namespace std;
const int N = 100010;
// 栈.栈初始的是tt == 0
int stk[N], tt;
int x;
// 插入一个x
stk[++tt] = x;
// 弹出
tt--;
// 判断栈是不是为空
if (tt > 0)
    bukong else kong

        // 取出来栈顶元素
        stk[tt];

// 队列
int q[N], hh, tt = -1;
// 在队尾插入元素,在队头弹出元素
// 插入
q[++tt] = x;
// 弹出
hh++; // 对头指针往后移动一位就是弹出了
// 判断是不是空的
if (hh <= tt) 非空
else kong
//取出对头元素
q[hh]
q[tt]
int main(void)
{

    return 0;
}

名言,现在应试教育考察的就是记忆力和毅力(所以英语好的都是考试总分最高的)

毅力就是能够坚持下来,持之以恒的背诵一个东西

记忆力和自制力.因为考试是一个现实的东西,凡事现实的东西都不可能现推(zxxy说考试的时候就是背诵,你考试的时候完全不可能有自己的思考)

事实就是这样,,我和y总英雄所见略同

看谁能够沉下心来好好背东西,去背一东西出来永远比你去想一个东西出来简单.

单调栈

单调栈常见的就一种题型,一个模型

给定一个序列,求一下每一个数左边,替他最近的,且比他小的数在什么地方

单调栈

从暴力循环的方法里面找一些特性,然后让查找变得更加的简单

先尝试用栈 里面存放指针i左边的数,,看看是不是有一些数字永远没有派上用场

有逆序关系的就把前面的用不着的点删掉,所以最后剩下的序列就是一个单调严格上升的序列了.

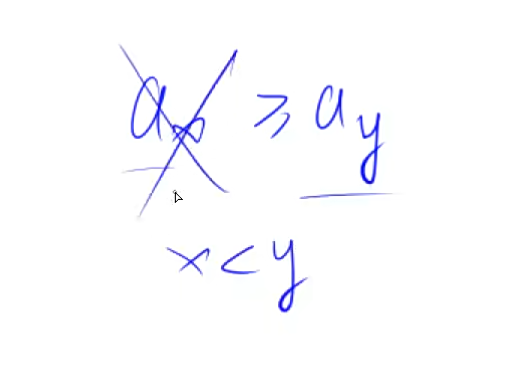
image-20241107173151378

第一次自己写的时候写出来了,说明脑袋里面还是有些许 while(不越界 && 某种条件)这种模式代码的印象.

同时注意栈初始为空的时候tt = 0;队列初始为空的时候tt = -1;

个人的思考过程加后续思考优化是这样子的

首先考虑一般的情况,如果新输入的x<= 栈顶元素,那么就弹栈.然后考虑弹栈还需要有一个终止条件就是栈为空.

**考虑&& 的短路原理,**写成这样

1
2
while (tt >= 1 && stk[tt] >= x)
            tt--;

把 ==栈不空的条件写在前面==,这样如果栈为空,就不会访问stk[tt]了

(因为栈为空,此时stk[tt]的访问是非法的

如果初始栈为空时,tt = -1;那么你访问空栈的栈顶就是stk[-1]在数组意义上时非法的.虽然编译器依旧通过.

如果初始栈为空时,tt = 0;那么你访问空栈的栈顶就是stk[0]在数组意义上时合法的,但是和上面的一段话类比,对于栈来说,你访问空栈的栈顶就是非法的.

)

这样子循环结束的时候,数学表达式上面应该是tt == 0 || stk[tt] < x(说实话,这种不好理解,反而让我混乱了,因此采用下面我介绍的形式)

具体情况可以看C++PrimerPlus第六版的图示

image-20241107181958683

循环结束的时候,具体情况应该分三种,就是图示里面的

1
2
3
expr1 == false && expr2 == true//栈为空,因此expr2根本就不会判断
expr1 == false && expr2== false//栈为空,因此expr2根本就不会判断
expr1 == true && expr2== false//栈不空,因此判断expr2

但是这里有短路原理,因此

此时,第一种情况和第二种情况//栈为空,因此expr2根本就不会判断

第三张情况//栈不空,因此判断expr2

对应本题的意思就是

while循环结束的时候

第一种情况,tt == 0(不管第二个表达式,事实上就是这种不管第二个表达式才保证了没有进行非法的访问),此时说明栈里面的元素都弹出了,,为什么元素都弹出了,中间没有停下来吗???

原因就是一直找到小于x的栈顶元素,所以tt一直减减直到tt == 0;

因此根据题意,返回-1;

第二种情况,tt >= 1 同时 此时栈顶元素小于x,因此就找到了最近的小于x的数,将栈顶元素输出就行.

这两种情况的进行的操作 就对应if else语句

(

这就是我对应的疑点,y总 的代码是这样的

1
2
3
4
if (tt >= 1)
    cout << stk[tt] << " ";
else
    cout << "-1 ";

似乎按照上面的我的逻辑来看,我的代码应该是这样 的

1
2
3
4
5
6
if (tt >= 1 && stk[tt] < x)
            cout << stk[tt] << " ";
else if (tt == 0 && stk[tt] >= x)
            cout << "-1 ";
else if(tt == 0 && stk[tt] < x)
    		cout << "-1 ";

==首先我将这段代码在测试里面run了,结果是Accepted==

说明我这么写也是可以的,但是大家为了图简便都是y总的写法

为什么可以呢???

因为在while循环结束后的后面,也就是说expr1 == true && expr2 == true已经不满足了,否则肯定还在while里面循环执行代码

因此肯定是

1
2
3
expr1 == false && expr2 == true//栈为空,因此expr2根本就不会判断
expr1 == false && expr2== false//栈为空,因此expr2根本就不会判断
expr1 == true && expr2== false//栈不空,因此判断expr2

而你只要写tt >= 1也就是expr1 == true,那么就一定是expr1 == true && expr2== false//栈不空,因此判断expr2的情况.

同理else也就是不满足tt >= 1也就是expr1 == false自然而然就是

1
2
expr1 == false && expr2 == true//栈为空,因此expr2根本就不会判断
expr1 == false && expr2== false//栈为空,因此expr2根本就不会判断

这两种情况合在一起了.(当然,expr2根本就不会进行判断)

)

最后要将x压入栈里面,就是stk[++tt] = x;(

前面的步骤是根据你输入的x来找里x最近的小于x的数,当然你本来是可以不弹出大于等于x的栈顶元素的,但是根据我们发现的性质有逆序关系的点就把前面的用不着的点删掉,所以前面的操作也是为了保持单调栈结构.

这一步压入栈是为了将这个输入的x作为后面查找的可能结果.)

注意算法题都给我用scanf和printf,速度比cin 和cout快十倍

时间复杂度:虽然有两重循环,我们关注栈顶指针tt,(这里为什么不关注tt的操作,难道是因为tt++ 和tt–和数组规模n没关系么,只有x和数据规模n有关系)

每一个数x的话,最多只会进栈一次,最多只会出栈一次,最多也就是2 * n的操作

因此整个算法的时间复杂度是O(n)

单调队列

常用题型就那么几道,最经典的是让你求滑动窗口的最大值或者最小值

思路是一样==的,先想一下暴力怎么做,然后挖掘其中的性质,把没有用的元素删掉,我们就得到单调性了==有单调性的话,我们就去求极值,就可以拿第一点或者最后一个点.就把本来要枚举一遍的时间复杂度变成O(1)了

具体来看