qingkongC

实战：斐波那契数列解法其二

学习了数组，我们来看看如何利用数组来计算斐波那契数列，这里采用动态规划的思想。

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

我们可以在一开始创建一个数组，然后从最开始的条件不断向后推导，从斐波那契数列的规律我们可以得知：

• fib[i] = fib[i - 1] + fib[i - 2]（这里fib代表斐波那契数列）

版权声明：本文为柏码知识库版权所有，禁止一切未经授权的转载、发布、出售等行为，违者将被追究法律责任。

原文链接：https://www.itbaima.cn/document/lqv77apvx82nkkio

转载自这位大佬，仅用于个人的学习和记笔记，无任何其他商业用途。如果造成了困扰和不便之处，请微信联系我。微信号BradTorres

我一定删除所有博文。

得到这样的一个关系（递推方程）就好办了，我们要求解数列第i个位置上的数，只需要知道i - 1和i - 2的值即可，这样，一个大问题，就分成了两个小问题，比如现在我们要求解斐波那契数列的第5个元素：

• fib[4] = fib[3] + fib[2]现在我们只需要知道fib[3]和fib[2]即可，那么我们接着来看：
• fib[3] = fib[2] + fib[1]以及fib[2] = fib[1] + fib[0]
• 由于fib[0]和fib[1]我们已经明确知道是1了，那么现在问题其实已经有结果了，把这些小问题的结果组合起来不就能得到原来大问题的结果了吗？

现在请你设计一个C语言程序，利用动态规划的思想解决斐波那契数列问题。

#include <stdio.h>

int main() {
    int target = 8;
    int dp[target];
    dp[1] = dp[0] = 1;
    for (int i = 2; i < target; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    printf("%d", dp[target - 1]);
    return 0;
}

————————————————

实战：打家劫舍

我们继续通过一道简单的算法题来强化动态规划思想。

来源：力扣（LeetCode）No.198 打家劫舍：https://leetcode.cn/problems/house-robber/

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

这道题我们也可以很轻松地按照上面的动态规划思路来处理，首先我们可以将问题分为子问题，比如现在有[2,7,9,3,1]五个房屋，这个问题看起来比较复杂，我们不妨先将大问题先简化成小问题，我们来看看只有N个房屋的情况：

• 假设现在只有[2]这一个房屋，那么很明显，我可以直接去偷一号房，得到2块钱，所以当有一个房子时最大能偷到2块钱。

• 假设现在有[2, 7]这两个房屋，那么很明显，我可以直接去偷二号房，得到7块钱，所以当有两个房子时最大能偷到7块钱。

• 假设现在只有

  [2, 7, 9]

  这三个房屋，我们就要来看看了，是先偷一号房再偷三号房好，还是只偷二号房好，根据前面的结论，如果我们偷了一号房，那么就可以继续偷三号房，并且得到的钱就是从一号房过来的钱+三号房的钱，也就是2+9块钱，但是如果只偷二号房的话，那么就只能得到7块钱，所以，三号房能够偷到的最大金额有以下关系（dp是我们求出的第i个房屋的最大偷钱数量，value表示房屋价值，max表示取括号中取最大的一个）：

  • dp[i] = max(dp[i - 1], dp[i - 2] + value[i]) -> 递推方程已得到

• 这样就不难求出：dp[2] = max(dp[1], dp[0] + value[i]) = dp[2] = max(7, 2 + 9) = dp[2] = 11，所以有三个房屋时最大的金额是11块钱。

• 所以，实际上我们只需要关心前面计算出来的盗窃最大值即可，而不需要关心前面到底是怎么在偷。

• 我们以同样的方式来计算四个房屋

  [2, 7, 9, 3]

  的情况：

  • dp[3] = max(dp[2], dp[1] + value[3]) = dp[3] = max(11, 7 + 3) = dp[3] = 11

• 所以，当有四个房屋时，我们依然采用先偷一后偷三的方案，不去偷四号，得到最大价值11块钱。

好了，现在思路已经出来了，我们直接上算法吧，现在请你实现下面的C语言程序：

#include <stdio.h>

int main() {
    int arr[] = {2,7,9,3,1}, size = 5, result;

    //请补充程序

    printf("%d", result);
}

力扣提交，建议各位小伙伴学习了函数和指针之后再回来看看，这里暂时可以跳过。

我写的

int rob(vector<int> &nums) {
    //nums相当于给出的arr
    int size = nums.size();
    if (size == 0) return 0;
    else if (size == 1)
        return nums[0];
    int result;
    int dp[size];
    dp[0] = nums[0];
    dp[1] = max(nums[0], nums[1]);
    for (int i = 2; i < size; i++)
        dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
    result = dp[size - 1];
    return result;
}

他写的

int max(int a, int b) {
    return a > b ? a : b;
}

int rob(int* nums, int numsSize){
    if(numsSize == 0) return 0;
    if(numsSize == 1) return nums[0];
    if(numsSize == 2) return max(nums[1], nums[0]);

    int dp[numsSize];
    dp[0] = nums[0];
    dp[1] = max(nums[1], nums[0]);

    for (int i = 2; i < numsSize; ++i) {
        dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
    }

    return dp[numsSize - 1];
}

————————————————

实战：回文串判断

“回文串”是一个正读和反读都一样的字符串，请你实现一个C语言程序，判断用户输入的字符串（仅出现英文字符）是否为“回文”串。

ABCBA 就是一个回文串，因为正读反读都是一样的

ABCA 就不是一个回文串，因为反着读不一样

int main() {
    char str[64];
    gets(str);
    //双指针，前后各一个
    int size = strlen(str);
    int i = 0, j = size - 1;
    while (i <= j) {
        if (str[i] != str[j]) {
            printf("false");
            return 0;
        }
        i++;
        j--;
    }

    printf("true");
}

实战：字符串匹配KMP算法

现在有两个字符串：

str1 = “abcdabbc”

str2 = “cda”

现在请你设计一个C语言程序，判断第一个字符串中是否包含了第二个字符串，比如上面的例子中，很明显第一个字符串包含了第二个字符串。

• 暴力解法

  int main() {
      char str1[64] = "abcdabbc";
      char str2[64] = "cda";
      unsigned long long len1 = strlen(str1);
      unsigned long long len2 = strlen(str2);
      int index = -1;
      int i = 0;
      int j = 0;
      while (i < len1) {
          if (j >= len2) {
              index = i - j;
              break;
          }
          if (str1[i] != str2[j]) {
              j = -1;
          }
  
          i++;
          j++;
      }
      //index是主串中子串的第一个字母出现的位置
      printf("%d\n", index);
  }

• KMP算法

往后复习到kmp结合代码随想录和考研408来看

？？？？？？？、

递归调用

我们的函数除了在其他地方被调用之外，也可以自己调用自己（好家伙，套娃是吧），这种玩法我们称为递归。

#include <stdio.h>

void test(){
    printf("Hello World!\n");
    test();   //函数自己在调用自己，这样的话下一轮又会进入到这个函数中
}

int main() {
    test();
}

我们可以尝试运行一下上面的程序，会发现程序直接无限打印Hello World!这个字符串，这是因为函数自己在调用自己，不断地重复进入到这个函数，理论情况下，它将永远都不会结束，而是无限地执行这个函数的内容。

但是到最后我们的程序还是终止了，这是因为函数调用有最大的深度限制，因为计算机不可能放任函数无限地进行下去。

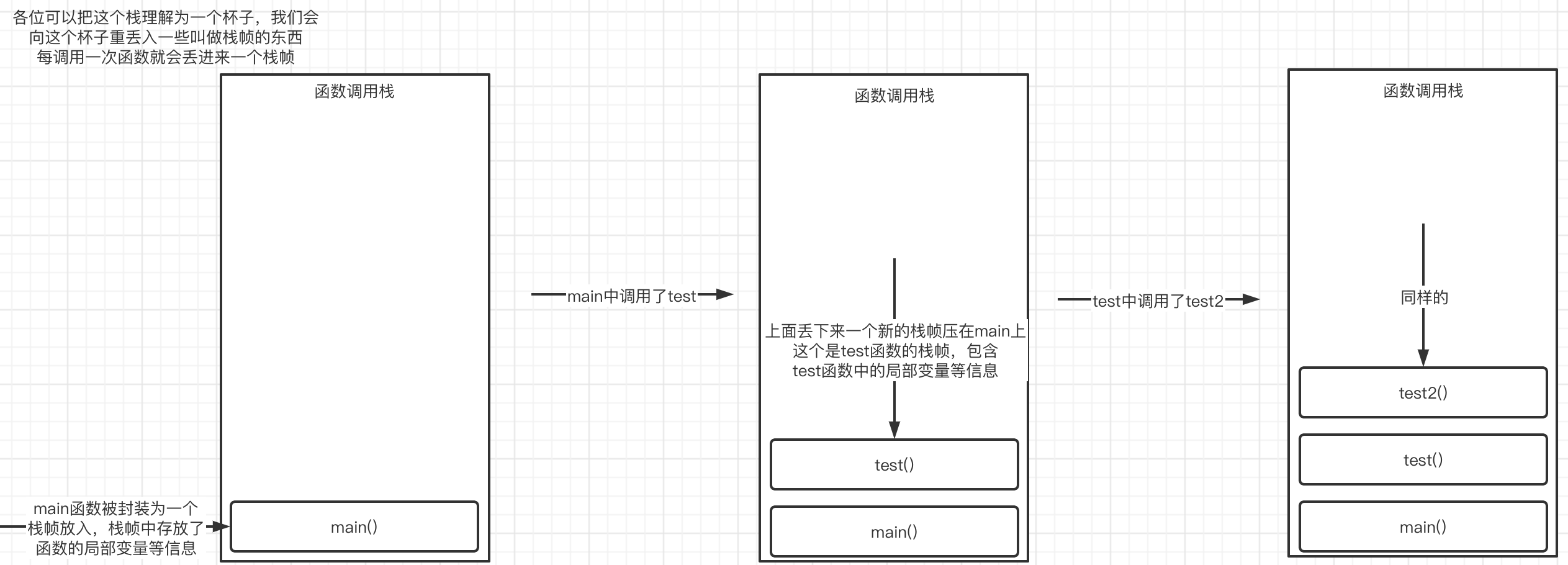
**（选学）**我们来大致了解一下函数的调用过程，实际上在程序运行时会有一个叫做**函数调用栈**的东西，它用于控制函数的调用：

#include <stdio.h>   //我们以下面的调用关系为例

void test2(){
    printf("giao");
}

void test(){
    test2();   //main -> test -> test2
  	printf("giao");
}

int main() {
    test();
  	printf("giao");
}

其实我们可以很轻易地看出整个调用关系，首先是从main函数进入，然后调用test函数，在test函数中又调用了test2函数，此时我们就需要等待test2函数执行完毕，test才能继续，而main则需要等待test执行完毕才能继续。而实际上这个过程是由函数调用栈在控制的：

而当test2函数执行完毕后，每个栈帧又依次从栈中出去：

当所有的栈全部出去之后，程序结束。

所以这也就不难解释为什么无限递归会导致程序出现错误，因为栈的空间有限，而函数又一直在进行自我调用，所以会导致不断地有新的栈帧进入，最后塞满整个栈的空间，就爆炸了，这种问题我们称为栈溢出（Stack Overflow）

当然，如果我们好好地按照规范使用递归操作，是非常方便的，比如我们现在需要求某个数的阶乘：

#include <stdio.h>

int test(int n);

int main() {
    printf("%d", test(3));
}

int test(int n){
    if(n == 1) return 1;   //因为不能无限制递归下去，所以我们这里添加一个结束条件，在n = 1时返回
    return test(n - 1) * n;  //每次都让n乘以其下一级的计算结果，下一级就是n-1了
}

通过给递归调用适当地添加结束条件，这样就不会无限循环了，并且我们的程序看起来无比简洁，那么它是如何执行的呢：

它看起来就像是一个先走到底部，然后拿到问题的钥匙后逐步返回的一个过程，并在返回的途中不断进行计算最后得到结果（妙啊）

所以，合理地使用递归反而是一件很有意思的事情。

实战：斐波那契数列解法其三

前面我们介绍了函数的递归调用，我们来看一个具体的实例吧，我们还是以解斐波那契数列为例。

既然每个数都是前两个数之和，那么我们是否也可以通过递归的形式不断划分进行计算呢？我们依然可以借鉴之前动态规划的思想，通过划分子问题，分而治之来完成计算。

实战：汉诺塔

什么是汉诺塔？

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始

按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

这三根柱子我们就依次命名为A、B、C，现在请你设计一个C语言程序，计算N阶（n片圆盘）汉诺塔移动操作的每一步。

这个问题看似很难，实际上我们也可以对每一步进行推理：

当汉诺塔只有1阶的情况下：直接把A上的圆盘移动到C，搞定。

当汉诺塔只有2阶的情况下：我们的最终目标还是需要将A柱最下面的圆盘丢到C，不过现在多了圆盘，我们得先把这个圆盘给处理了，所以我们得把这上面的1个圆盘丢到B上去，这样才能把A最下面的圆盘丢给C。然后再把B上面的1个圆盘丢到C上去

当汉诺塔只有3阶的情况下：我们的最终目标还是需要将A柱最下面的圆盘丢到C，不过现在多了圆盘，我们得先把这个圆盘给处理了，所以我们得把这上面的2个圆盘丢到B上去，这样才能把A最下面的圆盘丢给C。然后再把B上面的2个圆盘丢到C上

实际上我们发现，把A移动到C是一定要进行的，而在进行之前需要先把压在上面全部的圆盘全部放到B去。而移动之后也要把B上的圆盘全部移动到C上去。其实所有的情况下最终都会有一个n=1的情况，将A上的最后一个圆盘移动到C，只是多了一个前面的步骤和后面的步骤。

不过难点就是，怎么把A上的n-1个圆盘移动到B去呢？其实这时我们可以依靠C作为中间商，来帮助我们移动（比如n = 3，那么先把最上面的移动到C，然后把第二大的移动到B，再从C上把最小的移动到B上，这样就借助了C完成了两个圆盘的转移），而最后又怎么把B上的圆盘全部移到C去呢，这时就可以依靠A作为中间商，方法同理；实际上大问题最后都会变成n = 2时这样的小问题，只不过是要移动目标不同罢了。

只要想通了怎么去借助中间商进行移动，就很好写出程序了。

递归函数如下设计：

//a存放圆盘的初始柱子，b作为中间柱子存放使用，c作为目标柱子，n表示要从a移动到c的圆盘数
void hanoi(char a, char b, char c, int n){
    
}

现在我们来实现一下吧。

void move(char start, char end, int n){   //用于打印移动操作到控制台，start是起始柱子，end是结束柱子，n是哪一个圆盘
    printf("第%d个圆盘：%c --> %c\n", n, start, end);
}

void hanoi(char a, char b, char c, int n){  //刚进来的时候，B作为中间柱子，C作为目标柱子，要移动A上的n个圆盘到C去
    if(n == 1) {
        move(a, c, n);   //无论a,b,c如何变换，通过递归，最后都会变成一个n = 1的问题，直接移动就完事了
    } else{
        hanoi(a, c ,b, n - 1);  //首要目标是先把上面n-1个圆盘全部放到B去，这里就变换一下，让B作为目标柱子，C作为中间
        move(a, c, n);   //现在A上只剩下一个最大的圆盘了，接着把A最下方的一个圆盘移到C去
        hanoi(b, a, c, n - 1);   //最后需要把B上的全部搬到C上去，这里就可以以C为目标柱子，A为中间柱子
    }
}

简化一波：

void hanoi(char a, char b, char c, int n){
    if(n == 0) return;
    hanoi(a, c ,b, n - 1);
    printf("第%d个圆盘：%c --> %c\n", n, a, c);
    hanoi(b, a, c, n - 1);
}

看似如此复杂的问题，其实只需要4行就可以解决了。

实战：快速排序算法（选学）

有一个数组：

int arr[] = {4, 3, 8, 2, 1, 7, 5, 6, 9, 0};

现在请你设计一个C语言程序，对数组按照从小到大的顺序进行排序。这里我们使用冒泡排序的进阶版本——快速排序来完成，它的核心思想是分而治之，每一轮排序都会选出一个基准，一轮排序完成后，所以比基准小的数一定在左边，比基准大的数一定在右边，在分别通过同样的方法对左右两边的数组进行排序，不断划分，最后完成整个数组的排序。它的效率相比冒泡排序的双重for循环有所提升。

#include <stdio.h>

void quickSort(int arr[], int left, int right){  //arr是数组，left是起始下标，right是结束下标
    //请实现这一部分
}

int main() {
    int arr[] = {4, 3, 8, 2, 1, 7, 5, 6, 9, 0};
    quickSort(arr, 0, 9);  //10个数字下标就是0-9
    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr[i]);
    }
}

不过虽然这种排序算法很快，但是极端情况下（比如遇到了刚好倒序的数组）还是会退化成冒泡排序的。

————————————————