DS408+C408lg

第1章 绪论

第2章 线性表

第3章 栈、队列和数组

第4章 串

第5章 树与二叉树

第6章 图

第7章 查找

为什么要记录这个，事实上，不记录，我电脑的文件里面肯定找不到，然后就忘记了。就像笔记一样，好记性不如烂笔头。

顺序查找和二分查找

#include <bits/stdc++.h>
#include <deque>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
typedef int ElemType;
typedef struct {
    ElemType *elem;
    int TableLen;
} SSTable;
// 顺序查找
int Search_Seq(SSTable ST, ElemType key) {
    int i;
    for (i = 0; i < ST.TableLen && key != ST.elem[i]; i++)
        ;
    return i == ST.TableLen ? -1 : i;
}
//带哨兵的顺序查找
int Search_Seq1(SSTable ST, ElemType key) {
    ST.elem[0] = key;
    int i;
    for (i = ST.TableLen; key != ST.elem[i]; i--)
        ;
    return i;
}
//折半查找，二分查找
int Binary_Search(SSTable L, ElemType key) {
    int low = 0, high = L.TableLen - 1, mid;
    while (low <= high) {
        mid = low + (high - low >> 1);
        if (key > L.elem[mid]) low = mid + 1;
        else if (key < L .elem[mid])
            high = mid - 1;
        else
            return mid;
    }
    return -1;
}
int main() {
    SSTable t;
    t.TableLen = 12;
    t.elem = (ElemType *) calloc(t.TableLen, sizeof(ElemType));
    t.elem[11] = 33;
    t.elem[1] = 10;
    t.elem[2] = 38;
    t.elem[3] = 36;
    t.elem[4] = 325;
    t.elem[5] = 311;
    t.elem[6] = 3636;
    t.elem[7] = 355;
    t.elem[8] = 43;
    t.elem[9] = 3543;
    t.elem[10] = 322;
    cout << Search_Seq1(t, 43) << endl;
    return 0;
}

分块查找（顺序索引查找）

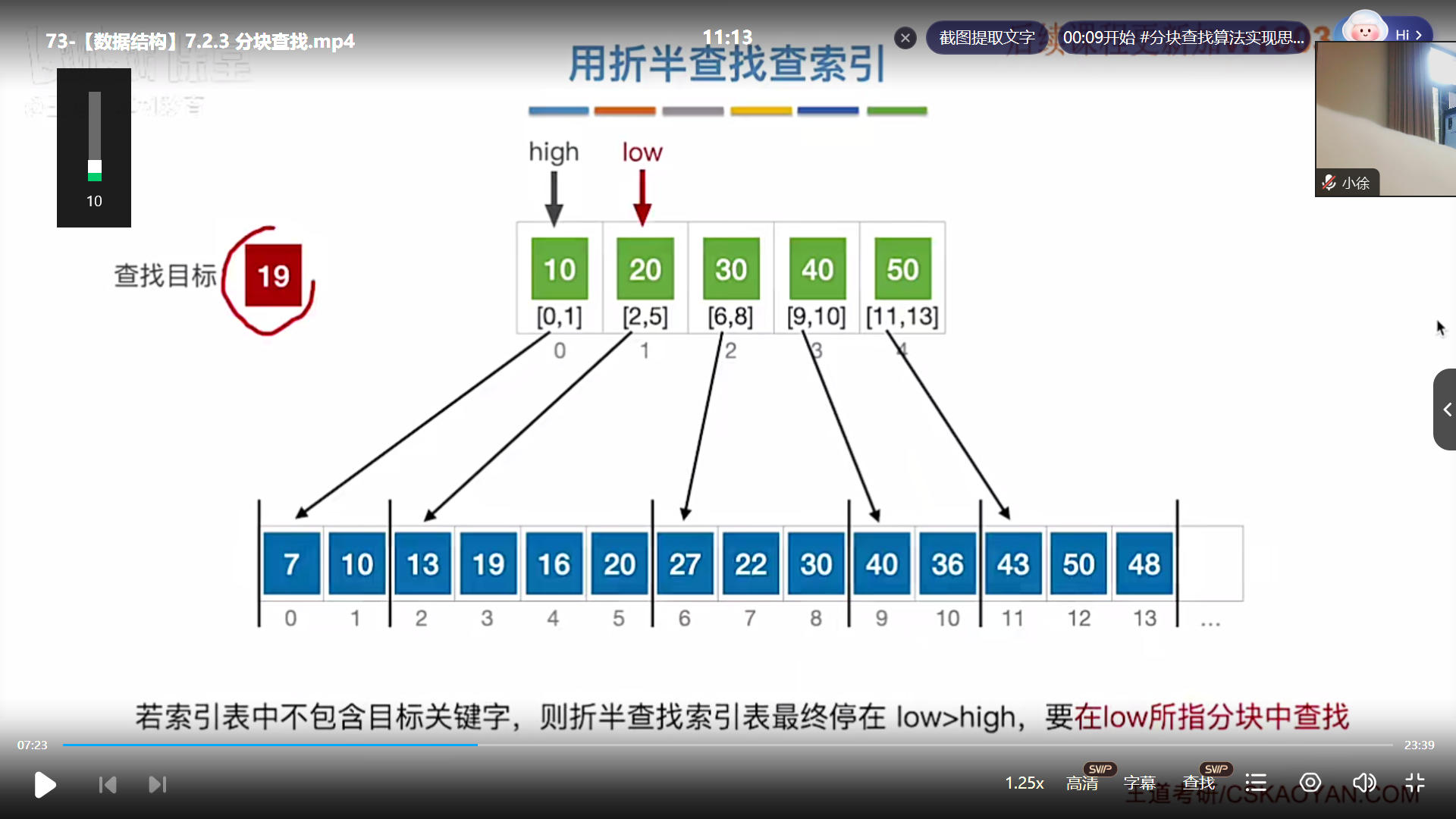
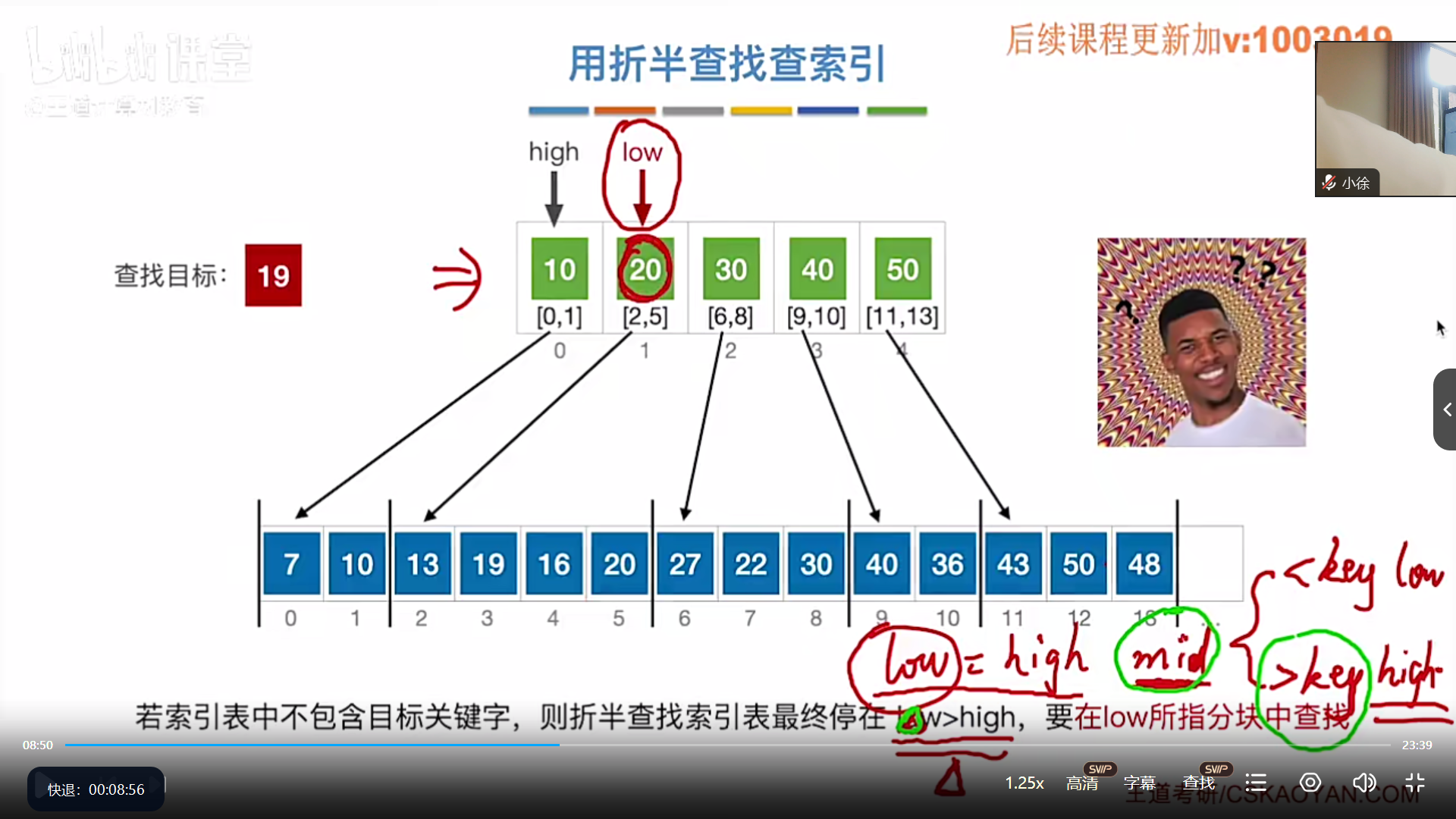
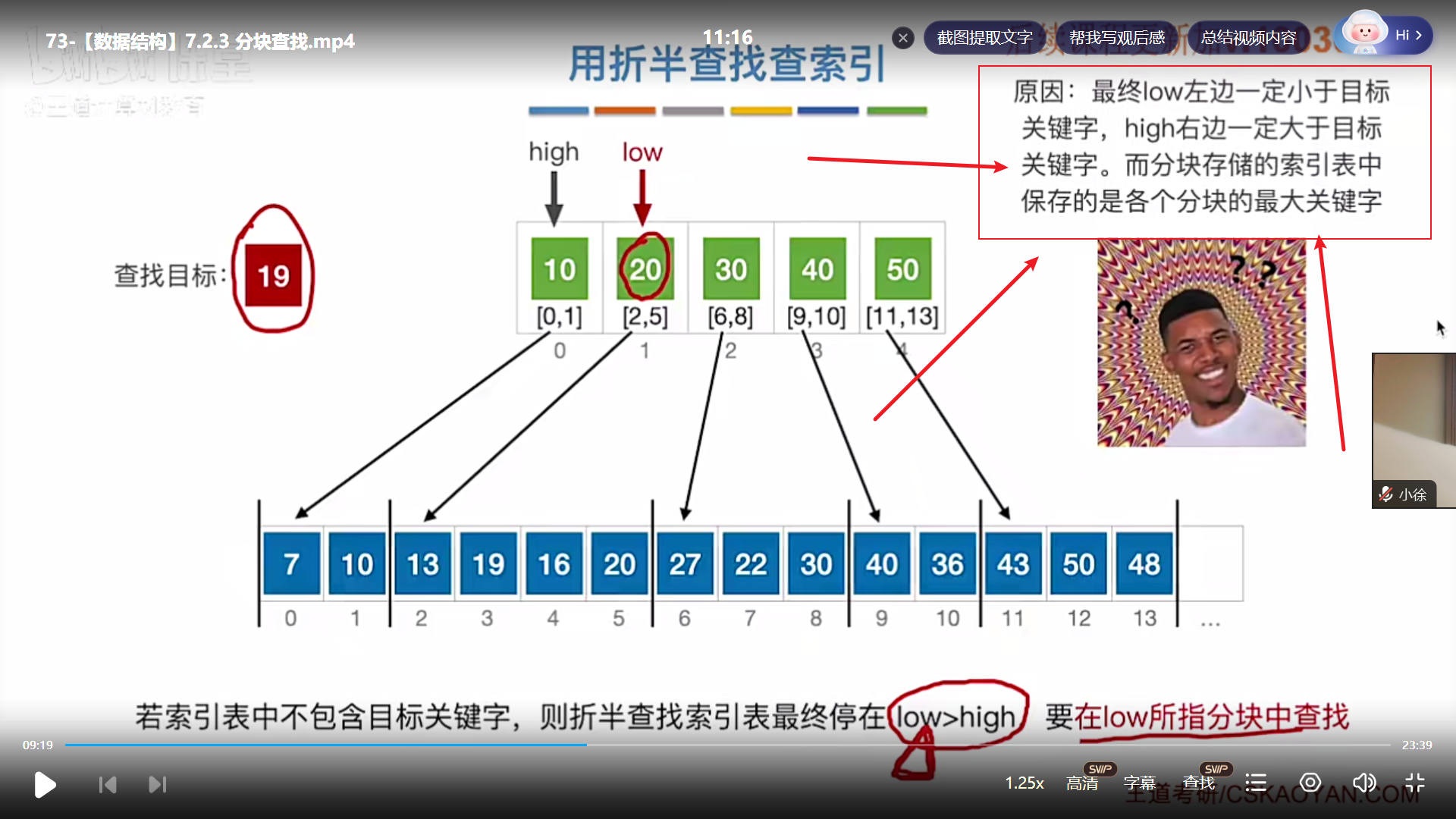
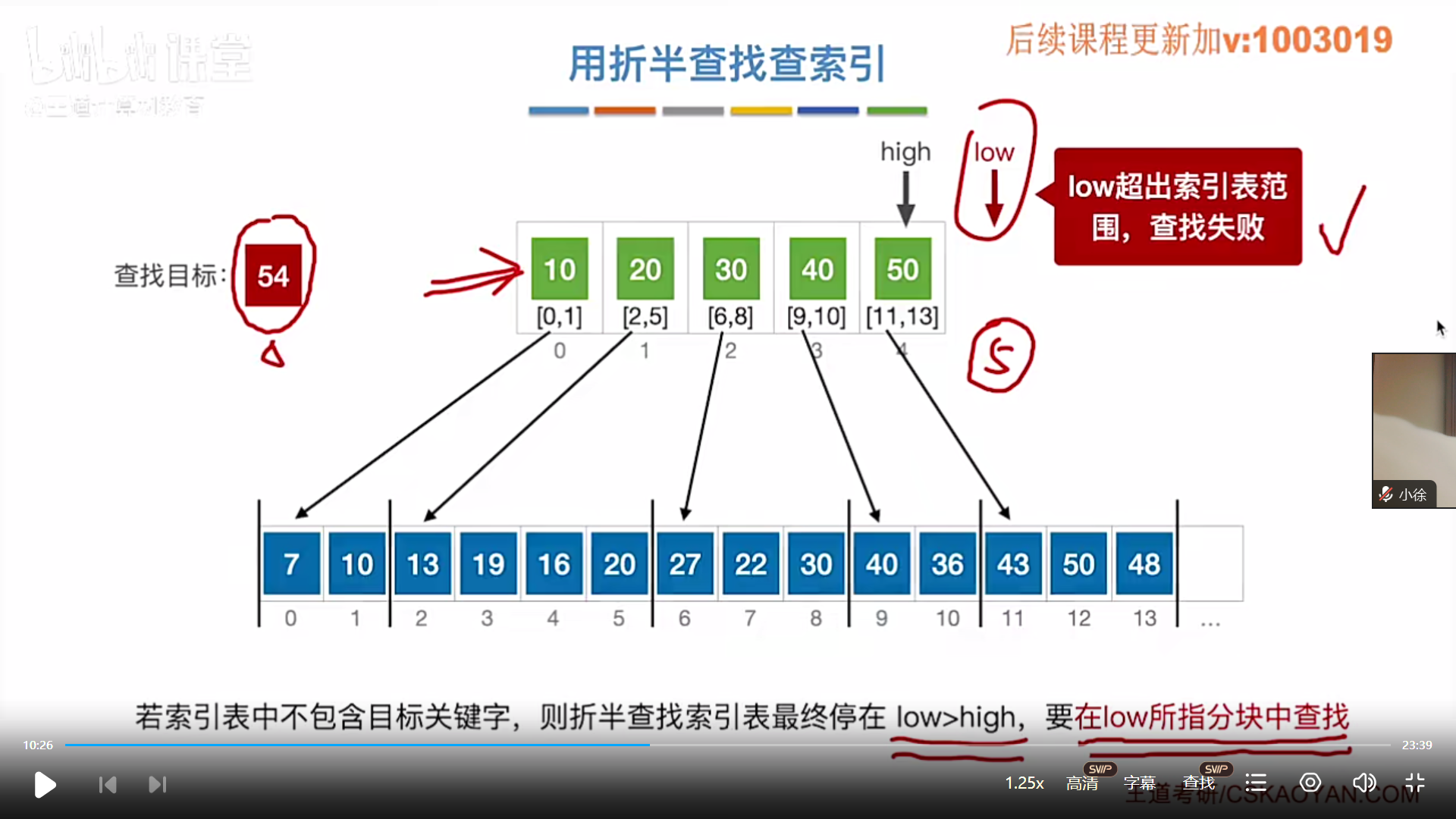
代码王道里面没有，

王道代码

#include <bits/stdc++.h>
#include <deque>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
typedef int ElemType;
//索引表
typedef struct{
    ElemType maxValue;
    int low, high;
}Index;
//顺序表存储实际元素
ElemType List[100];
int main() {
    return 0;
}

下面是网上找的

【查找系列_分块查找(索引顺序查找)[关键在于确定索引项位置]】 https://www.bilibili.com/video/BV1N24y1Z7eC/?share_source=copy_web&vd_source=82180e49f17daecf14bb6f246fc29cd0

#include <bits/stdc++.h>
#include <deque>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
typedef struct IndexElem {
    int maxKey;
    int low, high;
} IndexElem;
#define maxSize 5
//查找索引项
int searchIndexPos(IndexElem indexTable[], int target) {
    //这里的target比最右边的maxKey还大，也是王道讲的情况
    if (indexTable[maxSize - 1].maxKey < target)
        return -1;

    int low = 0, high = maxSize - 1;
    while (low <= high) {
        int mid = low + (high - low >> 1);
        if (target < indexTable[mid].maxKey)
            high = mid - 1;
        else if (target > indexTable[mid].maxKey)
            low = mid + 1;
        else
            return mid;
    }
    //查找失败,这里的return low就是王道讲的情况
    return low;
}
//分块查找
//indexElems是每块最大关键字组成的索引项表
//arr表示要查找的关键字序列
int blockSearch(IndexElem indexTable[], int arr[], int target) {
    int pos = searchIndexPos(indexTable, target);
    if (pos < 0)
        return -1;
    int low = indexTable[pos].low;
    int high = indexTable[pos].high;
    //顺序查找
    for (int i = low; i <= high; i++) {
        if (arr[i] == target) return i;
    }
    return -1;
}
int main() {
    int arr[] = {2, 1, 0, 3, 5, 4, 7, 6, 8, 9, 10, 11, 15, 18, 20};
    IndexElem indexTable[maxSize] = {
            {2, 0, 2},
            {
                    5,
                    3,
                    5,
            },
            {8, 6, 8},
            {11, 9, 11},
            {20, 12, 14}};
    printf("%d", blockSearch(indexTable, arr, 12));

    return 0;
}

二叉排序树

C++49的BST的插入

结构体定义

typedef struct tree_node {
	K key;
	struct tree_node* left;
	struct tree_node* right;

}TreeNode;

typedef struct {
	TreeNode* root;
	//把树都信息放在一个单独的结构体里面对他进行抽象
	//不过这里面只有一个指向根节点的指针，你也可以加 int size 等等，看你的需求了
}BST;
//API

插入实现，其实这个tree就是二级指针

void bst_insert(BST* tree, K key) {
	

	//查找位置 ,先判断一下数里面有没有这个key，没有才创建节点。调用bst_search????
	//一般实现bst里面key的数值是唯一的，不允许重复
	TreeNode* parent = NULL;
	TreeNode* curr = tree->root;
	int cmp;
	while (curr) {
		cmp = key - curr->key;
		if (cmp < 0) {
			parent = curr;
			curr = curr->left;
		}
		else if (cmp > 0) {
			parent = curr;
			curr = curr->right;
		}
		else {
			
			return;
		}
	}
	//curr == NULL,，没有这个key，要分配空间开始插入了
	TreeNode* newNode = calloc(1, sizeof(TreeNode));
	if (!newNode) {
		fprintf(stderr, "malloc failed in bst_insert\n");
		//printf("malloc failed in bst_insert\n");
		exit(1);
	}
	newNode->key = key;

	//相当于链表的尾插法，链表的尾插法就是考虑两种情况 1.前面没有结点，链表为空 2. 前面有结点，链表不为空 
	//事实上，只要有跟节点，那么新的节点只能插入在根节点左子树或者右子树，不可能和链表一样插入在第一个节点前面，因此不用考虑插入的节点在根节点之前的情况
	//BST为空。。没有根节点，那么插入的节点就是跟节点

	if (parent == NULL) {
		tree->root = newNode;
	}
	//插入的位置在根节点后面
	else if (cmp < 0) parent->left = newNode;
	else  parent->right = newNode;
	return;
	// 这个不是二叉平衡数
}

王道代码

#include <bits/stdc++.h>
#include <deque>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
#define SIZE(a) (sizeof(a) / sizeof(a[0]))
//二叉排序树节点
typedef struct BSTNode {
    int key;
    struct BSTNode *lchild, *rchild;
} BSTNode, *BSTree;

//在二叉排序树中查找值为key的节点
BSTNode *BST_Search(BSTree T, int key) {
    while (T != NULL && key != T->key) {
        if (key < T->key) T = T->lchild;
        else
            T = T->rchild;
    }
    //走到这里 ，说明找到了T,而且他还满足key == T->key
    //当时如果T == NULL的话，也是直接走到这里。
    // T可能一开始为NULL,也可能是没查到，即查到了空结点
    return T;
}
//在二叉排序树中查找值为key的节点， 递归实现
BSTNode *BSTSearch(BSTree T, int key) {
    if (T == NULL) return NULL;
    if (key < T->key) BSTSearch(T->lchild, key);
    else if (key > T->key)
        BSTSearch(T->rchild, key);
    else
        return T;
}
//在二叉排序树插入关键字为k的新结点(递归实现)
//个人感觉非递归实现要找前一个结点，让他的指针指向新插入的节点，是不是难了一些
int BST_Insert(BSTree &T, int k) {
    //边界条件
    //既是一开始树为空，就让他直接插入
    // 又是找到了对应的叶子结点的下面的空结点的位置
    // 在空结点的位置插入
    // 因为在递归里面，这个T其实是可以指，或者说遍历所有节点的
    // 相当于node
    // 因为要修改指针，从指向NULL到指向新结点，
    if (T == NULL) {
        T = (BSTNode *) calloc(1, sizeof(BSTNode));
        T->key = k;
        return 1;
    }//递归公式
    else if (k < T->key)
        BST_Insert(T->lchild, k);
    else if (k > T->key)
        BST_Insert(T->rchild, k);
    else
        return 0;//树中存在相同的结点，插入失败
}
//非递归实现，好像要找前一个结点，好难，不想思考情况，不管了
// 如果不用引用&，好像要用二级指针，所以引用&万岁
// 不会写，不想动脑
// 见C++49里面写的，完全记不清在干嘛了
//难死了，以后都用递归写BST的插入
int BSTInsert(BSTree &T, int k) {
}
void Create_BST(BSTree &T, int str[], int n) {
    T = NULL;//初始时T为空树
    int i = 0;
    while (i < n) {//依次将每个关键字插入到二叉排序树当众
        BST_Insert(T, str[i]);
        i++;
    }
}
int main() {
    BSTree T;
    int str[] = {50, 66, 60, 26, 21, 30, 70, 68};
    int size = SIZE(str);
    printf("%d\n", size);
    Create_BST(T, str, size);
    return 0;
}

王道代码没有删除操作，网上找的一个讲的封神的老师的视频

【懒猫老师-数据结构-(58)二叉排序树的删除(二叉查找树)】 https://www.bilibili.com/video/BV1EK4y1e7UY/?share_source=copy_web&vd_source=82180e49f17daecf14bb6f246fc29cd0

完成了他这一p作业一

#include <bits/stdc++.h>
#include <deque>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;
#define SIZE(a) (sizeof(a) / sizeof(a[0]))
//二叉排序树节点
typedef struct BSTNode {
    int key;
    struct BSTNode *lchild, *rchild;
} BSTNode, *BSTree;

//在二叉排序树中查找值为key的节点
BSTNode *BST_Search(BSTree T, int key) {
    while (T != NULL && key != T->key) {
        if (key < T->key) T = T->lchild;
        else
            T = T->rchild;
    }
    //走到这里 ，说明找到了T,而且他还满足key == T->key
    //当时如果T == NULL的话，也是直接走到这里。
    // T可能一开始为NULL,也可能是没查到，即查到了空结点
    return T;
}
//在二叉排序树中查找值为key的节点， 递归实现
BSTNode *BSTSearch(BSTree T, int key) {
    if (T == NULL) return NULL;
    if (key < T->key) BSTSearch(T->lchild, key);
    else if (key > T->key)
        BSTSearch(T->rchild, key);
    else
        return T;
}
//在二叉排序树插入关键字为k的新结点(递归实现)
//个人感觉非递归实现要找前一个结点，让他的指针指向新插入的节点，是不是难了一些
int BST_Insert(BSTree &T, int k) {
    //边界条件
    //既是一开始树为空，就让他直接插入
    // 又是找到了对应的叶子结点的下面的空结点的位置
    // 在空结点的位置插入
    // 因为在递归里面，这个T其实是可以指，或者说遍历所有节点的
    // 相当于node
    // 因为要修改指针，从指向NULL到指向新结点，
    if (T == NULL) {
        T = (BSTNode *) calloc(1, sizeof(BSTNode));
        T->key = k;
        return 1;
    }//递归公式
    else if (k < T->key)
        BST_Insert(T->lchild, k);
    else if (k > T->key)
        BST_Insert(T->rchild, k);
    else
        return 0;//树中存在相同的结点，插入失败
}
//非递归实现，好像要找前一个结点，好难，不想思考情况，不管了
// 如果不用引用&，好像要用二级指针，所以引用&万岁
// 不会写，不想动脑
// 见C++49里面写的，完全记不清在干嘛了
//难死了，以后都用递归写BST的插入
int BSTInsert(BSTree &T, int k) {
}
//神作，讲的很好
// 【懒猫老师-数据结构-(58)二叉排序树的删除(二叉查找树)】 https://www.bilibili.com/video/BV1EK4y1e7UY/?share_source=copy_web&vd_source=82180e49f17daecf14bb6f246fc29cd0
void deleteNode(BSTree &T) {
    if (T->lchild == NULL && T->rchild == NULL) {
        //叶子结点
        BSTNode *p = T;
        //因为T是引用类型，所以此时的T和上一层递归传下来的
        //T.lchild或者T.rchild指向同一片内存空间
        // 可以理解为此时的T是上一层传下来的T.lchild的别名
        // 对同一片内存空间的赋值自然会相互影响，
        // 这就是引用&的实质
        // 老师说的话，T采用引用&，那么T的值一旦发生了任何改变
        // T的值可以被传出去，传给上一级调用它的那个实际参数，


        T = NULL;
        delete (p);
    } else if (T->rchild == NULL)//右子树为空
    {
        BSTNode *p = T;
        T = T->lchild;
        delete (p);
    } else if (T->lchild == NULL)//左子树为空
    {
        BSTNode *p = T;
        //感觉这里的理解，可以看成链表的删除图示
        // 这里的T就是上一层，也就是父节点的孩子指针，
        // 让父节点的孩子指针指向他的孩子的孩子，即指向T->child
        //也就是T = T->rchild;
        T = T->rchild;
        delete (p);
    } else {//左右子树都不为空
        BSTNode *parent = T;
        BSTNode *pre = T->lchild;//因为左右子树都不为空，所以pre肯定不为空
        //转左，然后向右到尽头(找到左子树中最大结点)
        while (pre->rchild) {
            parent = pre;
            pre = pre->rchild;
        }
        //赋值
        T->key = pre->key;//pre指向要删除的结点的前驱，用它替换删除数据

        //删除pre结点，parent->rchild = NULL;这样就错误了
        if (parent != T)                 //判断是否执行了上述while循环
            parent->rchild = pre->lchild;//执行了while循环，接parent的右子树
        else                             //
            //突然发现这句话有个更好的理解，
            // 就是把赋值符号右边的指针变量，也就是指向某个类型的指针
            // 看作是地址，如本代码看作是pre左孩子的地址
            // 也就是将pre左孩子的地址赋值给了parent的左孩子指针
            // 就好理解，等于是parent的左孩子指针指向了pre的左孩子，
            parent->lchild = pre->lchild;//没执行了while循环，接parent的左子树
        delete (pre);
    }
}
//删除操作不讲吗，自己上网查了一个
//下面这个是伪代码，BST的删除算法
bool deleteBST(BSTree &T, int key) {
    if (T == NULL)
        return false;
    else if (T->key == key) {
        deleteNode(T);//找到关键词，删除一个结点
        return true;
    } else if (key < T->key)
        deleteBST(T->lchild, key);
    else
        deleteBST(T->rchild, key);
}
void Create_BST(BSTree &T, int str[], int n) {
    T = NULL;//初始时T为空树
    int i = 0;
    while (i < n) {//依次将每个关键字插入到二叉排序树当众
        BST_Insert(T, str[i]);
        i++;
    }
}
void visit(BSTree T) {
    printf("%4d", T->key);
}
void inOrder(BSTree T) {
    if (T == NULL) return;
    inOrder(T->lchild);
    visit(T);
    inOrder(T->rchild);
}
int main() {
    BSTree T;
    int str[] = {38, 12, 34, 56, 13, 6, 98, 3, 17, 40, 78};
    int size = SIZE(str);
    printf("%d\n", size);
    Create_BST(T, str, size);
    inOrder(T);
    printf("\n");

    bool result = deleteBST(T, 999);
    inOrder(T);
    if (result)
        printf("\nTrue");
    else
        printf("\nFalse");

    return 0;
}

完成了他这一p作业二

在不增加结点情况下，将二叉排序树转换成有序双向链表

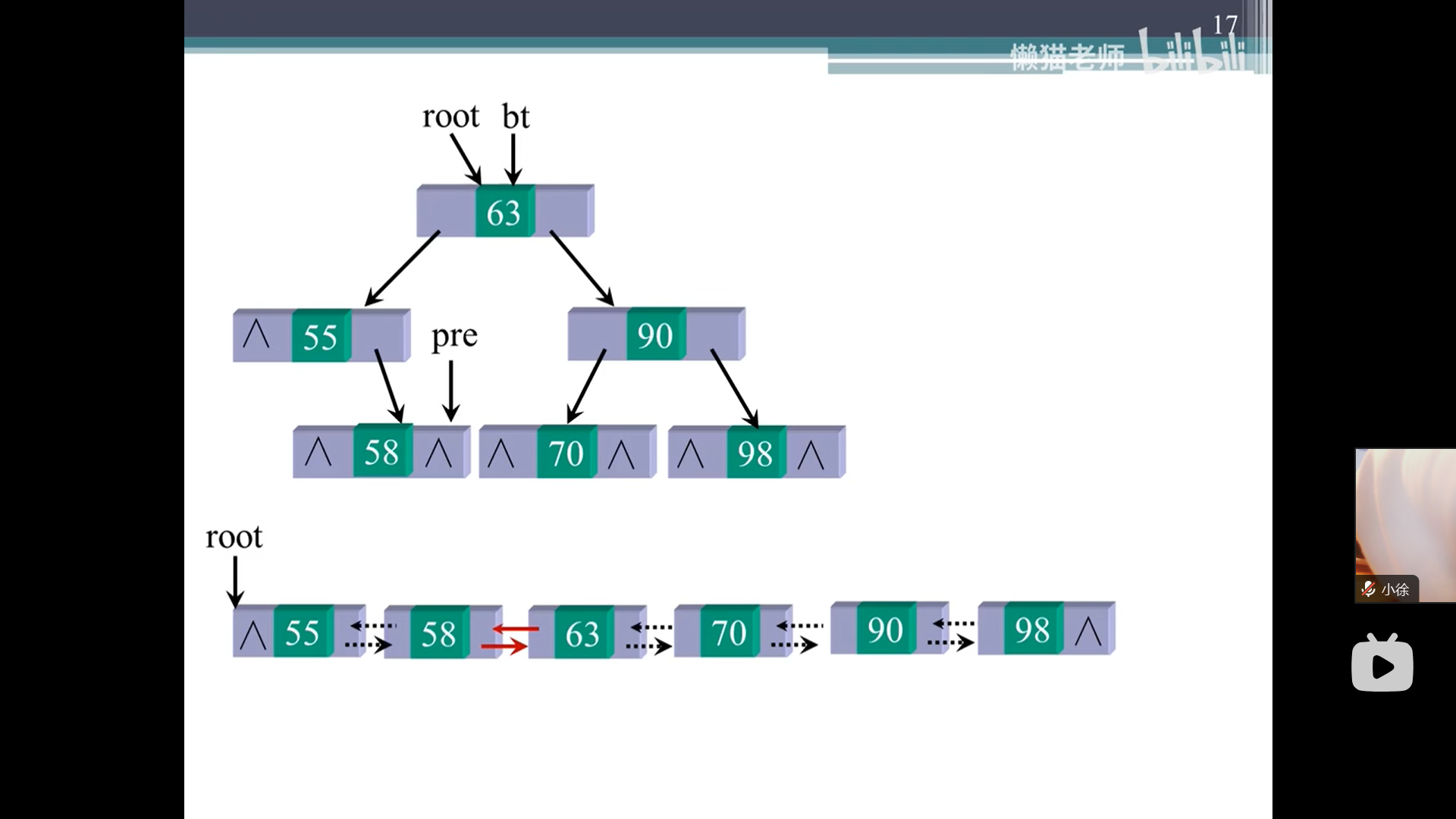
题目要求不能创建任何新的结点，只需要调整指针的指向，那么就意味着可直接利用二叉树的结点，通过变更结点的左右孩子的指向，来生成双链表的逻辑关系。问题就变成了：

找当前root结点的左孩子最大的结点left_max，和找当前root结点的右孩子最大的结点right_max然后变更各自的指向，依次递归，然后变更指针指向关系：

left_max->rchild= root;
root->lchild = left_max;
right_max->lchild = root;
root->rchild = right_max;

————————————————

解题算法

第8章 排序